OLS assumption

 Fixing the issue in assumption of OLS step by step or one by one

by: Editor in Chief

    

 424 Shares     

Posted by: admin 2 months ago

(0 Comments)

Hi, I want to raise the issue related to know whether your OLS is ok or not. 

Linear

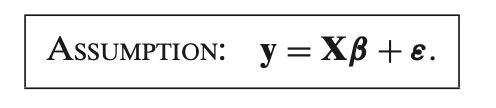
This assumption is the **linear regression model** equation, which states that the **observed values** of the dependent variable $y$ are modeled as a **linear combination of the predictors** $X$ plus an **error term** $ϵ$.

Breaking it down:

1. **$y$**: This is the vector of observed values for the dependent variable (the outcome we are trying to predict or explain).

2. **$X\beta$**:
- $X$ is the matrix of predictors (independent variables), where each row represents an observation, and each column represents a different predictor.
- $\beta$ is the vector of coefficients associated with each predictor, representing the strength and direction of the relationship between each predictor and the outcome $y$.

Together, $X\beta$ represents the **predicted values** based on the linear relationship between $y$ and the predictors.

3. **$ϵ$**: This is the **error term** or **residuals**. It captures the **deviation of the observed values $y$ from the predicted values $X\beta$**. The error term represents all factors affecting $y$ that are not captured by the predictors in $X$.

### In Simple Terms
This assumption states that:
- The relationship between the predictors (independent variables) and the outcome (dependent variable) is **linear**.
- The outcome $y$ can be expressed as the sum of the predicted part (from the linear combination of $X\beta$) and the random error $ϵ$.

This is a core assumption in **linear regression** models and forms the basis for estimating the coefficients $\beta$ using methods like ordinary least squares (OLS).

Fullrank

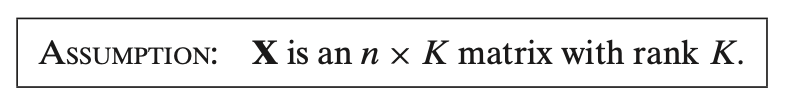
This assumption states that **$X$**, the matrix of predictors (independent variables), is an **$n\times K$** matrix with **rank $K$**. Here’s what this means in the context of linear regression:

1. **$X$ as an $n\times K$ Matrix**:
- **$n$** is the number of observations (rows) in the dataset.
- **$K$** is the number of predictors (columns), including any constant term if one is added to the model.
- So, $X$ is a matrix where each row represents an observation, and each column represents a predictor.

2. **Rank $K$**:
- The **rank** of a matrix is the number of linearly independent columns. In this case, having **rank $K$** means that all $K$ columns (predictors) in $X$ are **linearly independent**.
- **Linear independence** means that no column in $X$ can be written as a linear combination of the other columns.
- This assumption is crucial for estimating the coefficients $\beta$ in a linear regression model. If the columns of $X$ are not linearly independent (i.e., if $X$ has rank less than $K$), the matrix $X^{\prime }X$ (used in calculating the regression coefficients) becomes **singular** and cannot be inverted. This situation is known as **perfect multicollinearity**.

### Why This Assumption is Important
- **Ensures Uniqueness of Coefficients**: With full rank $K$, the coefficients $\beta$ in the regression model $y=X\beta +ϵ$ can be uniquely estimated.
- **Avoids Multicollinearity**: If the rank of $X$ is less than $K$, it means there is perfect multicollinearity, which would prevent us from estimating the regression model properly.

### In Simple Terms
This assumption requires that the predictors in $X$ are independent of each other and that there is no exact linear relationship among them. This independence allows the regression model to produce a unique and valid solution for the coefficients $\beta$.

Exogeneity

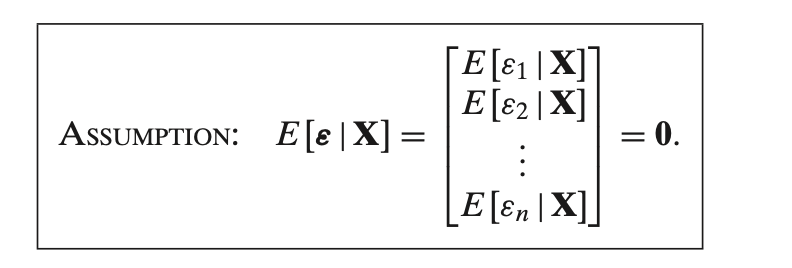
This assumption states that the **expected value of the error term $ϵ$, given the predictor matrix $X$, is zero**. Mathematically:

$$E[ϵ|X]=\left[\begin{array}{c}E[{ϵ}_1|X]\\ E[{ϵ}_2|X]\\ ⋮\\ E[{ϵ}_n|X]\end{array}\right]=0$$

### What This Means
1. **Zero Conditional Mean Assumption**:
- This assumption implies that the errors $ϵ$ are **uncorrelated with the predictor variables** $X$.
- For each observation $i$, the expected value of the error term ${ϵ}_i$, given the predictors $X$, is zero. This means that, on average, the error term does not systematically deviate from zero for any value of $X$.

2. **Implication for Unbiasedness**:
- This assumption is crucial for the **unbiasedness** of the Ordinary Least Squares (OLS) estimator. If $E[ϵ|X]=0$, it ensures that the predictor variables are not correlated with the errors, which means that the estimated coefficients $\beta$ will not be biased by omitted variables or endogeneity.
- In other words, this assumption implies that **the predictors capture all relevant information** about the outcome variable, and any remaining error is random and unrelated to the predictors.

### In Simple Terms
This assumption states that the error term has **no systematic relationship with the predictors**. It ensures that the predictors $X$ explain everything they can about the outcome variable $y$, and any leftover error (or noise) is purely random. This is essential for making sure that the OLS estimates are accurate and unbiased.

Yes, the assumption $E[ϵ|X]=0$ is directly related to the concept of **endogeneity**.

- **Endogeneity** occurs when there is a correlation between the predictors (independent variables) $X$ and the error term $ϵ$.
- **Exogeneity**, by contrast, means that the predictors are not correlated with the error term. This is precisely what the assumption $E[ϵ|X]=0$ implies: the errors are uncorrelated with the predictors, ensuring **exogeneity**.

If this assumption does **not** hold (i.e., if $E[ϵ|X]\ne 0$), we have **endogeneity**. Endogeneity can arise for several reasons, such as:

1. **Omitted Variable Bias**: If an important variable that affects both $X$ and $y$ is omitted from the model, it can lead to correlation between $X$ and $ϵ$.
2. **Simultaneity**: If there is a two-way causal relationship between $X$ and $y$, where $X$ influences $y$ and $y$ simultaneously influences $X$, endogeneity occurs.
3. **Measurement Error**: If there are errors in measuring $X$, these errors can correlate with the error term, introducing endogeneity.

### Why Endogeneity is Problematic
When endogeneity is present, the **OLS estimates** of the coefficients are **biased and inconsistent**. This means the estimated coefficients do not reflect the true relationship between $X$ and $y$, making inference and predictions unreliable.

### Addressing Endogeneity
To deal with endogeneity, econometricians often use techniques such as:
- **Instrumental Variables (IV)**: Introducing variables that are correlated with $X$ but uncorrelated with $ϵ$.
- **Fixed Effects Models**: In panel data, fixed effects can control for omitted variables that are constant over time.
- **Control Variables**: Including additional relevant variables that may be causing endogeneity due to omitted variable bias.

In summary, the assumption $E[ϵ|X]=0$ ensures **exogeneity**. If this assumption fails, endogeneity is present, which compromises the reliability of OLS regression results.

Homokedasticy

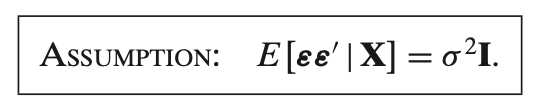
This assumption states that the **variance-covariance matrix** of the error term $ϵ$, conditional on the predictor matrix $X$, is equal to ${\sigma }^{2}I$. Here’s a breakdown of what this means:

1. **Variance-Covariance Matrix of Errors**:
- $E[ϵ{ϵ}^{\prime }|X]$ represents the **variance-covariance matrix** of the error terms $ϵ$ given $X$.
- This matrix contains the variances of the errors on the diagonal and the covariances between different error terms on the off-diagonal.

2. **Assumption of Homoskedasticity**:
- The expression ${\sigma }^{2}I$ implies that the error terms have a **constant variance** ${\sigma }^2$ for each observation. This is known as **homoskedasticity**.
- **Homoskedasticity** means that the variance of the error term is the same across all values of $X$.

3. **No Correlation Between Errors (Independence)**:
- The identity matrix $I$ indicates that there are **zeros in all off-diagonal elements** of the variance-covariance matrix. This implies that the error terms are **uncorrelated with each other**.
- In other words, there is **no covariance** between the errors for different observations, meaning that each error term is independent of the others.

### Why This Assumption Matters
This assumption is crucial in **ordinary least squares (OLS) regression** because:
- It ensures that the **OLS estimators are efficient** (have the lowest variance among linear unbiased estimators) under the Gauss-Markov theorem.
- If this assumption does not hold (i.e., if there is heteroskedasticity or autocorrelation), the standard errors of the estimated coefficients might be incorrect, leading to unreliable statistical inference (such as incorrect confidence intervals and hypothesis tests).

### In Simple Terms
This assumption means that:
- **Each error term has the same variance** (no heteroskedasticity).
- **Error terms are independent** of each other (no autocorrelation).

In practical terms, it implies that the errors are spread out evenly and independently across observations, which helps ensure reliable OLS estimates. If this assumption is violated, adjustments such as **robust standard errors** or **generalized least squares (GLS)** may be used to obtain valid inference.

What is matrix identity

A **matrix identity** (often called the **identity matrix**) is a **square matrix** with ones on the **main diagonal** (from the top left to the bottom right) and zeros in all other positions. It serves as the equivalent of the number "1" in matrix operations, meaning that multiplying any matrix by the identity matrix leaves the original matrix unchanged.

### Properties of the Identity Matrix

1. **Notation and Structure**:
- The identity matrix is usually denoted by $I$.
- For an $n\times n$ identity matrix (where $n$ is the number of rows and columns), we write $I_n$.
- A 2x2 identity matrix looks like this:
$$I_2=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$
- A 3x3 identity matrix looks like this:
$$I_3=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

2. **Multiplicative Identity**:
- The identity matrix behaves similarly to the number "1" in regular multiplication. For any matrix $A$ of compatible dimensions (e.g., an $n\times n$ matrix), multiplying $A$ by $I$ leaves $A$ unchanged:
$$AI=IA=A$$
- This property is fundamental in linear algebra and matrix operations, as it means that the identity matrix does not alter other matrices when used in multiplication.

3. **Role in Inverses**:
- The identity matrix is also important in defining **matrix inverses**. For a matrix $A$, if there exists a matrix $B$ such that:
$$AB=BA=I$$
then $B$ is called the **inverse of $A$**, often denoted as $A^{-1}$.

4. **Diagonal Structure**:
- The identity matrix has **1s on its main diagonal** and **0s elsewhere**. This structure makes it a diagonal matrix and a special case of the more general class of matrices called **diagonal matrices**.

### Summary
The identity matrix is a square matrix that acts as a neutral element in matrix multiplication, leaving other matrices unchanged when multiplied by them. It plays a fundamental role in linear algebra, especially in matrix operations involving multiplication, inverses, and transformations.

Normality

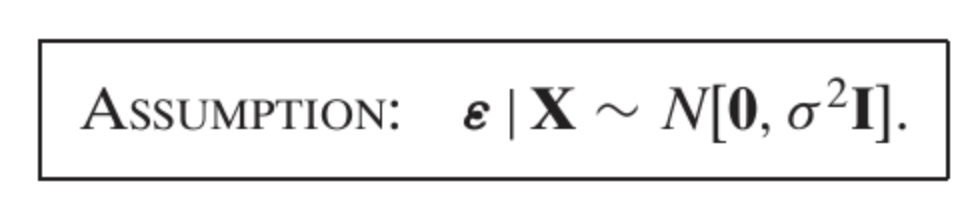
This assumption specifies that the **error term** $ϵ$, given the matrix of predictors $X$, follows a **normal distribution** with **mean 0** and **constant variance** ${\sigma }^2$.

Breaking down the notation:

1. **$ϵ|X$**: This notation means that the error term $ϵ$ is being considered **conditional on the predictor matrix** $X$. In other words, given the values of the predictors, we are making an assumption about the distribution of the error term.

2. **$N[0,{\sigma }^{2}I]$**: This indicates that $ϵ$ is **normally distributed** with:
- **Mean 0**: The expected value of $ϵ$ is 0, implying that errors are centered around zero and do not systematically bias the predictions.
- **Variance ${\sigma }^{2}I$**: The variance of $ϵ$ is **constant and equal to ${\sigma }^2$ for all observations**, where $I$ is the identity matrix. This means there is **no heteroskedasticity** (constant variance) and **no correlation** between the error terms of different observations.

### In Simple Terms
This assumption means:
- **Errors are normally distributed** around zero.
- **Errors have constant variance** ${\sigma }^2$ across all observations.
- **Errors are independent** of each other (no correlation).

This assumption is commonly used in **ordinary least squares (OLS) regression** and other linear models to simplify estimation and inference, as it ensures that estimators are **unbiased and efficient** under the classical linear regression model.